X線作業主任者の過去問の解説：管理（2024年10月）

ここでは、2024年（令和6年）10月公表の過去問のうち「エックス線の管理に関する知識（問1～問10）」について解説いたします。

それぞれの科目の解説は、下記ページからどうぞ。

◆X線作業主任者の過去問の解説：管理（2024年10月）
◆X線作業主任者の過去問の解説：法令（2024年10月）
◆X線作業主任者の過去問の解説：測定（2024年10月）
◆X線作業主任者の過去問の解説：生体（2024年10月）

問１　エックス線に関する次の記述のうち、正しいものはどれか。

（１）エックス線の光子は、電子と同じ質量をもつ。
（２）エックス線は、直接電離放射線である。
（３）連続エックス線は、高エネルギー電子が原子核近傍の強い電場を通過するとき急に減速され、運動エネルギーの一部を電磁波の形で放出するものである。
（４）エックス線管の管電圧と管電流が一定の場合、ターゲット元素の原子番号が大きいほど、連続エックス線の最短波長は短くなる。
（５）制動エックス線は、軌道電子が、エネルギー準位の高い軌道から低い軌道へと遷移するときに発生する。

答え（３）
（１）は誤り。エックス線の光子は質量を持たない粒子であり、電子のような質量はありません。
（２）は誤り。エックス線は間接電離放射線であり、直接電離放射線（アルファ線など）とは異なります。
（３）正しい。連続エックス線（制動放射）は、高速電子が原子核近傍の強い電場で急減速した際に発生します。
（４）は誤り。連続エックス線の最短波長は、管電圧に依存します。「ターゲット元素の原子番号が大きいほど、連続エックス線の最短波長は短くなる」というのは誤りです。
（５）は誤り。制動エックス線ではなく、特性エックス線が軌道電子の遷移によって発生します。

問２　特性エックス線に関する次の記述のうち、正しいものはどれか。

（１）特性エックス線の波長は、ターゲット元素の原子番号が大きくなると長くなる。
（２）特性エックス線は、原子核のエネルギー準位の遷移に伴い、原子核から放出される。
（３）管電圧が、K系列の特性エックス線を発生させるのに必要な最小値であるK励起電圧を下回るときは、他の系列の特性エックス線も発生することはない。
（４）K殻電子が電離されたことによって特性エックス線が発生することをオージェ効果という。
（５）ターゲット元素がタングステンの場合のK励起電圧は、タングステンより原子番号の小さい銅やモリブデンの場合に比べて高い。

答え（５）
（１）は誤り。ターゲット元素の原子番号が大きいほど特性エックス線の波長は短くなります。
（２）は誤り。特性エックス線は、電子軌道のエネルギー準位の遷移に伴い発生し、原子核の遷移は関係ありません。
（３）は誤り。K励起電圧を下回る場合、K系列は発生しませんが、L系列などの他の特性エックス線が発生する可能性はあります。
（４）は誤り。オージェ効果は、電子放出に関連する現象であり、特性エックス線の発生とは異なります。
（５）正しい。タングステンの原子番号は銅やモリブデンより大きいため、K励起電圧も高くなります。

問３　エックス線装置の管電圧を一定にして、管電流を増加させた場合に、発生する連続エックス線に認められる変化として、正しいものは次のうちどれか。

（１）全強度は、管電流に比例して大きくなる。
（２）最大強度を示す波長は、短くなる。
（３）最短波長は、短くなる。
（４）最大エネルギーは、管電流に比例して大きくなる。
（５）発生効率は、管電流にほぼ比例して高くなる。

答え（１）
（１）正しい。管電流が増加すると、発生するエックス線の全強度は管電流に比例して増加します。
（２）誤り。最大強度を示す波長は管電圧によって決まり、管電流では変化しません。
（３）誤り。最短波長も管電圧によって決まります。
（４）誤り。最大エネルギーは管電流ではなく管電圧に比例します。
（５）誤り。発生効率は管電圧やターゲット材料に依存し、管電流には比例しません。

問４　エックス線と物質との相互作用に関する次の記述のうち、正しいものはどれか。

（１）コンプトン効果により散乱されるエックス線の中には、入射エックス線より波長の短いものがある。
（２）コンプトン効果は、必ず特性エックス線の発生を伴う。
（３）光電効果が生じる確率は、入射エックス線のエネルギーが増大すると、コンプトン効果に比べて急激に低下する。
（４）光電効果により光子エネルギーが原子に吸収されて光子は消滅し、このとき入射エックス線に等しい運動エネルギーを持つ電子が放出される。
（５）電子対生成は、入射エックス線のエネルギーが、電子1個の静止質量に相当するエネルギー以上であるときに生じる。

答え（３）
（１）誤り。コンプトン効果による散乱で波長が短くなることはありません。
（２）誤り。コンプトン効果と特性エックス線の発生は直接的な関係がありません。
（３）正しい。一方で、コンプトン効果が生じる確率は、緩やかに低下します。
（４）誤り。光電効果では、放出される電子のエネルギーは入射光子エネルギーから結合エネルギーを引いた値になります。
（５）誤り。電子対生成は、入射エックス線のエネルギーが、電子2個分に相当するエネルギー以上であるときに生じます。

問５　単ーエネルギーの細いエックス線束が物体を透過するときの減弱に関する次の記述のうち、誤っているものはどれか。

（１）鉄の半価層は、鉛の半価層より大きい。
（２）半価層の値は、エックス線の線量率が高くなっても変化しない。
（３）軟エックス線の場合は、硬エックス線の場合より、半価層の値が小さい。
（４）エネルギーが1MeV程度までのエックス線に対する鉄の半価層の値は、エックス線のエネルギーが高くなるほど大きくなる。
（５）1/10価層H（cm）と半価層h（cm）との間には、次の関係がある。
H＝(log_e2/log_e10)h

答え（５）
（１）（２）（３）（４）は正しい。
（５）は誤り。H＝(log_e10/log_e2)hの関係があります。

問６　エックス線の散乱に関する次の文中の［　　］内に入れるAからCの語句又は数値の組合せとして、正しいものは（１）～（５）のうちどれか。

「エックス線装置を用い、管電圧200kVで、厚さが20mmの鋼板及びアルミニウム板のそれぞれにエックス線のビームを垂直に照射し、散乱角135°の方向の後方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、［　A　］の後方散乱線の方が小さかった。
次に、同じ照射条件で、鋼板について、散乱角120°及び135°の方向の後方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、［　B　］の方向の方が小さかった。
また、同じ照射条件で、鋼板について、散乱角30°及び60°の方向の前方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、［　C　］の方向の方が小さかった。」

（１）A：アルミニウム板　B：120°　C：60°
（２）A：アルミニウム板　B：135°　C：30°
（３）A：アルミニウム板　B：135°　C：60°
（４）A：鋼板　B：120°　C：60°
（５）A：鋼板　B：135°　C：30°

答え（４）
A：鋼板の後方散乱線の方がアルミニウム板より小さいです。
B：散乱角が120°の方が135°より小さいです。
C：前方散乱では散乱角60°の方が30°より小さいです。

問７　単一エネルギーで太い線束のエックス線が物質を透過するときの減弱及び再生係数（ビルドアップ係数）に関する次の記述のうち、誤っているものはどれか。

（１）再生係数は、1未満となることはない。
（２）再生係数は、線束の広がりが大きいほど大きくなる。
（３）再生係数は、入射エックス線のエネルギーや物質の種類によって異なる。
（４）再生係数は、物質の厚さが厚くなるほど大きくなる。
（５）太い線束のエックス線では、細い線束のエックス線より減弱曲線の勾配は緩やかになり、見かけ上、減弱係数が大きくなる。

答え（５）
（１）（２）（３）（４）は正しい。
（５）誤り。太い線束のエックス線では、物質を透過するエックス線に、散乱エックス線が加わるため、見かけ上、減弱係数が小さくなります（あまり減弱していないように見える）。

問８　エックス線の利用に関する次のAからDの記述について、正しいものの全て　の組合せは（１）～（５）のうちどれか。

A　被検査物体にエックス線を照射し、透過線の強度の違いから内部の構造を調べる手法をラジオグラフィ（透過撮影法）という。
B　空港の手荷物検査装置は、被検査物体にエックス線を照射した結果発生する特性エックス線のエネルギーを分析することにより、手荷物の検査を行う装置である。
C　後方散乱線を利用する検査方法では、エックス線フィルム（又はエックス線検出器）を、被検査物体の裏側ではなく、エックス線源と同じ側に配置して検査を行う。
D　溶接による残留応力など金属にひずみがあると原子が規則正しく並んでいる格子間隔が正常値からずれるので、エックス線の回折を利用して、ひずみの度合いを測定することができる。

（１）A，B，C
（２）A，C，D
（３）A，D
（４）B，C
（５）C，D

答え（２）
A　正しい。透過撮影法（ラジオグラフィ）はこの説明に該当します。
B　誤り。空港の手荷物検査装置はエックス線透過強度の違いを解析するものであり、特性エックス線のエネルギー分析は行いません。
C　正しい。後方散乱を利用する場合、検出器はエックス線源と同じ側に配置します。
D　正しい。エックス線回折を利用して金属のひずみを測定できます。

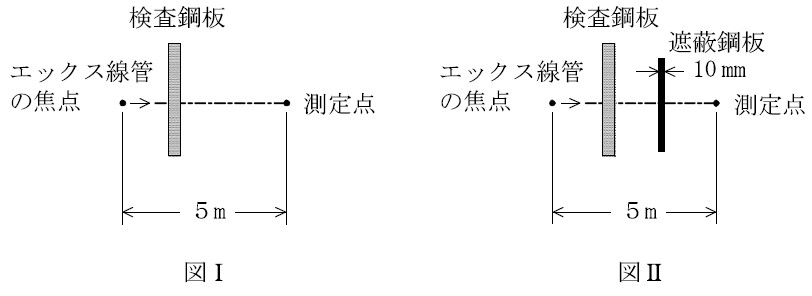
問９　図Ⅰのように、鋼板に垂直に細い線束のエックス線を照射し、エックス線管の焦点から5mの位置で、透過したエックス線の1cm量当量率を測定したところ、16mSv/hであった。
次に図Ⅱのように、この線束を厚さ10mmの鋼板で遮蔽し、同じ位置で1cm線量当量率を測定したところ4mSv/hとなった。
この位置における1cm線量当量率を0.5mSv/h以下とするために必要な遮蔽鋼板の最小の厚さは次のうちどれか。
ただし、エックス線の実効エネルギーは変わらないものとする。
また、散乱線の影響は無いものとする。

（１）15mm
（２）20mm
（３）25mm
（４）30mm
（５）45mm

答え（３）
まず、鋼板の半価層hがわからないので、指数関数減弱の式 I ＝ I₀(1/2)^x/hを使って求めます。
問題文より、「鋼板を透過したエックス線の1cm線量当量率は16mSv/h」ですが、「厚さ10mmの鋼板で遮蔽し、測定したところ4mSv/hとなった」ことがわかります。
これらの数値を代入すると次のようになります。

4 [mSv/h] ＝ 16 [mSv/h] (1/2)^{10 [mm] / h [mm]}
4 [mSv/h] / 16 [mSv/h] ＝ (1/2)^{10 [mm] / h [mm]}
(1/2) × (1/2) ＝ (1/2)^{10 [mm] / h [mm]}
(1/2)² ＝ (1/2)^{10 [mm] / h [mm]}

左辺と右辺は、(1/2)の部分が同じなので、指数の部分にも同じ数字が入ります。
指数の部分を抜き出して計算すると、次のようになります。

2 ＝ 10 [mm] / h [mm]
h ＝ 5

つまり、鋼板の半価層hは5mmです。
続いて、「同じ位置における1cm線量当量率を0.5mSv/h以下とするために必要な遮蔽鋼板の最小の厚さx」を、指数関数減弱の式を使って求めます。

0.5 [mSv/h] ＝ 16 [mSv/h] (1/2) ^{x [mm] / 5 [mm]}
0.5 [mSv/h] / 16 [mSv/h] ＝ (1/2) ^{x [mm] / 5 [mm]}
(1/2) [mSv/h] / 16 [mSv/h] ＝ (1/2) ^{x [mm] / 5 [mm]}
(1/32) [mSv/h] ＝ (1/2) ^{x [mm] / 5 [mm]}
(1/2) × (1/2) × (1/2) × (1/2) × (1/2)＝ (1/2) ^{x [mm] / 5 [mm]}
(1/2) ⁵＝(1/2) ^{x [mm] / 5 [mm]}

左辺と右辺は、(1/2)の部分が同じなので、指数の部分にも同じ数字が入ります。
指数の部分を抜き出して計算すると、次のようになります。

5 ＝ x [mm] / 5 [mm]
5 × 5 [mm] ＝ x [mm]
x [mm] ＝ 5 × 5 [mm]
x [mm] ＝ 25 [mm]

つまり、厚さ25mm以上の遮蔽鋼板を使えば、透過後の1cm線量当量率を0.5mSv/h以下にすることができます。
よって、（３）25mmが正解です。

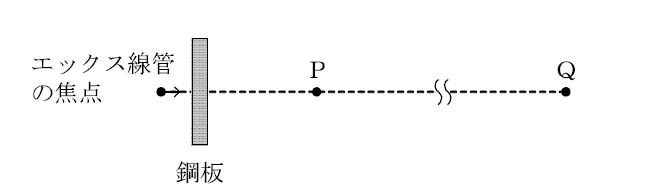
問１０　下図のように、エックス線装置を用いて鋼板の透過写真撮影を行うとき、エックス線管の焦点から3mの距離のP点における写真撮影中の1cm線量当量率は0.2mSv/hである。
エックス線管の焦点とP点を結ぶ直線上で、焦点からP点の方向に15mの距離にあるQ点を管理区域の境界の外側になるようにすることができる1週間当たりの撮影可能な写真の枚数として、最大のものは（１）～（５）のうちどれか。
ただし、露出時間は1枚の撮影について120秒間であり、3か月は13週とする。

（１）290枚/週
（２）375枚/週
（３）430枚/週
（４）530枚/週
（５）675枚/週

答え（２）
この問題は、図のQ点が管理区域の境界線の外側にあるとき、1週間当たりの撮影可能な写真の最大枚数を求めるものです。
なお、管理区域とは、3か月あたり1.3mSvを超えるおそれのある区域です。

まず、週の撮影枚数をNとし、3か月当たりの全撮影時間を計算します。

全撮影時間＝1枚当たりの露出時間×週の撮影枚数×3か月の週数
　＝120/3,600[h/枚]×N[枚/週]×13[週/3か月]
　＝(1,560/3,600)N[h/3か月]

割り切れない場合は、分数のまま計算した方が後の計算式がスッキリします。

次に、P点における3か月当たりの線量当量を計算します。

線量当量＝線量当量率×全撮影時間
　＝0.2[mSv/h]×(1,560/3,600)N[h/3か月]
　＝(312/3,600)N[mSv/3か月]

それでは、逆2乗則を使って、週の撮影枚数Nを求めましょう。
逆2乗則は、強度が距離の2乗に反比例して減少する法則なので、次のような計算式で表されます。

強度(P点)/強度(Q点)＝距離(Q点)²/距離(P点)²

(312/3,600)N[mSv/3か月]/1.3[mSv/3か月]＝15²[m]/3²[m]
312N/(1.3×3,600)＝225/9
312N＝225×1.3×3,600/9
312N＝117,000
N＝117,000/312
N＝375

したがって、Q点を管理区域の境界の外側になる1週間当たりの撮影可能な写真の最大枚数は、（２）375枚/週です。

« X線作業主任者の過去問の解説：生体（2024年4月） X線作業主任者の過去問の解説：法令（2024年10月） »

X線作業主任者の過去問の解説：管理（2024年10月） | エックス線作業主任者講習会・通信講座