X線作業主任者の過去問の解説：管理（2015年4月）

ここでは、2015年（平成27年）4月公表の過去問のうち「エックス線の管理に関する知識（問1～問10）」について解説いたします。

それぞれの科目の解説は、下記ページからどうぞ。

◆X線作業主任者の過去問の解説：管理（2015年4月）
◆X線作業主任者の過去問の解説：法令（2015年4月）
◆X線作業主任者の過去問の解説：測定（2015年4月）
◆X線作業主任者の過去問の解説：生体（2015年4月）

問1　エックス線管及びエックス線の発生に関する次の記述のうち、正しいものはどれか。

（1）エックス線管から発生するエックス線は、制動放射による連続エックス線であり、特性エックス線は含まれていない。
（2）陽極には、発生したエックス線を集束させるために集束筒（集束カップ）が設けられている。
（3）陽極のターゲットに衝突した熱電子の運動エネルギーの10～30％がエックス線に変換され、残りの大部分は熱に変わる。
（4）エックス線の発生効率は、ターゲット元素の原子番号と管電圧の積に比例する。
（5）陽極のターゲット上で、電子が衝突しエックス線が発生する部分である実効焦点の寸法が大きいほど、像質のよい写真を撮影することができる。

問2　特性エックス線に関する次の記述のうち、誤っているものはどれか。

（1）特性エックス線の波長は、ターゲット元素の原子番号が大きくなると長くなる。
（2）特性エックス線は、線スペクトルを示す。
（3）特性エックス線を発生させるために必要な管電圧の最小値を励起電圧という。
（4）ターゲット元素がタングステンの場合のK励起電圧は、タングステンより原子番号の小さい銅やモリブデンの場合に比べて高い。
（5）管電圧を上げると、特性エックス線の強度は増大するが、波長は変わらない。

問3　エックス線管から発生する連続エックス線の全強度Iを実験的に示した式は、次のうちどれか。
ただし、V：管電圧、i：管電流、Z：ターゲット元素の原子番号、k：比例定数とする。

（1）I=kiV²Z
（2）I=kiVZ²
（3）I=ki²VZ
（4）I=kiVZ
（5）I=ki²V/Z

問4　エックス線と物質との相互作用に関する次の記述のうち、誤っているものはどれか。

（1）エックス線が光子として原子に衝突したとき、軌道電子が光子のエネルギーを吸収して原子の外に飛び出し、光子が消滅する現象を光電効果という。
（2）光電効果が起こる確率は、入射エックス線のエネルギーが高くなるほど大きくなる。
（3）エックス線が光子として軌道電子と衝突し、電子が原子の外に飛び出し、光子が運動の方向を変える現象をコンプトン効果という。
（4）コンプトン効果によって散乱したエックス線の波長は、入射エックス線の波長より長い。
（5）高エネルギーのエックス線が光子として原子核近傍の電場を通過するとき、電子と陽電子の対を生成し、光子が消滅する現象を電子対生成という。

問5　単一エネルギーの細いエックス線束が物体を透過するときの減弱に関する次の記述のうち、正しいものはどれか。

（1）半価層h（cm）と減弱係数μ（cm^-1）との間には、μh=log_e2の関係がある。
（2）半価層は、エックス線のエネルギーが変わっても変化しない。
（3）半価層は、エックス線の線量率が高くなると厚くなる。
（4）軟エックス線の場合は、硬エックス線の場合より半価層が厚い。
（5）半価層の値は、物体を構成する元素の種類が変わっても変化しない。

問6　エックス線の利用に関する次のAからDまでの記述について、正しいものすべての組合せは（1）～（5）のうちどれか。

A　被検査物体にエックス線を照射し、透過線の強度の違いから内部の構造を調べる手法をラジオグラフィ（透過撮影法）という。
B　空港の手荷物検査装置は、被検査物体にエックス線を照射した結果発生する特性エックス線のエネルギーを分析することにより、手荷物の検査を行う装置である。
C　後方散乱線を利用する検査方法では、エックス線フィルム（又はエックス線検出器）を、被検査物体の裏側ではなく、エックス線源と同じ側に配置して検査を行う。
D　溶接による残留応力など金属にひずみがあると格子間隔が正常値からずれるので、エックス線の回折を利用して、ひずみの度合いを測定することができる。

（1）A，B，C
（2）A，C，D
（3）A，D
（4）B，C
（5）C，D

問7　エックス線を鋼板に照射したときの散乱線に関する次の記述のうち、正しいものはどれか。
ただし、特に記述したもの以外の条件はすべて同一とする。

（1）散乱線の空気カーマ率は、散乱角が90°のときに最も大きい。
（2）前方散乱線の空気カーマ率は、鋼板の板厚が増すに従って増加する。
（3）前方散乱線の空気カーマ率は、散乱角が大きくなるに従って増加する。
（4）後方散乱線の空気カーマ率は、鋼板の板厚が増すに従って滅少する。
（5）後方散乱線の空気カーマ率は、管電圧が高くなるに従って増加する。

問8　エックス線装置を使用する作業場における管理区域を設定するための外部放射線の測定に関する次の記述のうち、誤っているものはどれか。

（1）測定器は、方向依存性が大きく、感度が高く、かつ、測定可能な下限線量が小さなものを用いる。
（2）作業者が立ち入る区域で線源に最も近い箇所又は遮へいの薄い箇所等、1 cm線量当量又は1 cm線量当量率が最大になると予測される箇所を測定箇所に含める。
（3）作業者が常に作業している箇所を測定箇所に含める。
（4）壁等の構造物によって区切られた境界の近辺の箇所を測定箇所に含める。
（5）位置によって測定値の変化が大きいと予測される場合は、測定点を密にとる。

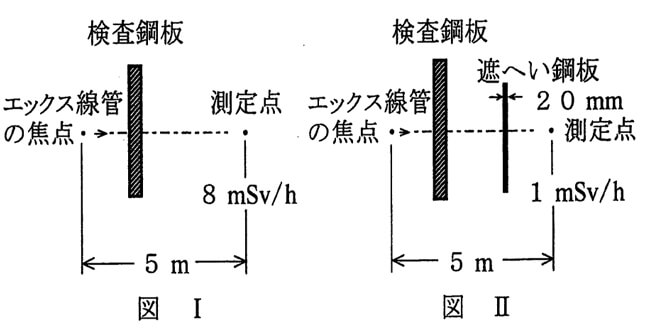
問9　下図Ⅰのように、検査鋼板に垂直に細い線束のエックス線を照射し、エックス線管の焦点から5 mの位置で、透過したエックス線の1 cm線量当量率を測定したところ、8 mSv/hであった。
次に下図Ⅱのように、この線束を厚さ20 mmの鋼板で遮へいし、同じ位置で1 cm線量当量率を測定したところ1 mSv/hとなった。
この遮へい鋼板を厚いものに替えて、同じ位置における1 cm線量当量率を0.5 mSv/h以下とするために必要な遮へい鋼板の最小の厚さは（1）～（5）のうちどれか。
ただし、エックス線の実効エネルギーは変わらないものとする。
また、散乱線の影響は無いものとする。
なお、log_e2=0.69とする。

（1）21 mm
（2）23 mm
（3）25 mm
（4）27 mm
（5）30 mm

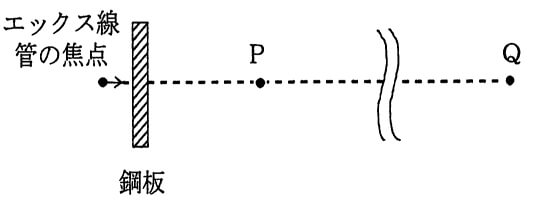
問10　下図のように、エックス線装置を用いて鋼板の透過写真撮影を行うとき、エックス線管の焦点から3 mの距離のP点における写真撮影中の1 cm線量当量率は0.3 mSv/hである。
露出時間が1枚につき110秒の写真を週300枚撮影するとき、Q点を管理区域の境界線の外側になるようにするために必要な焦点からQ点までの距離として、最も短いものは（1）～（5）のうちどれか。
ただし、3か月は13週とする。

（1）10 m
（2）12 m
（3）14 m
（4）16 m
（5）18 m

Tweet