X線作業主任者の過去問の解説:管理(2021年4月)
ここでは、2021年(令和3年)4月公表の過去問のうち「エックス線の管理に関する知識(問1~問10)」について解説いたします。
それぞれの科目の解説は、下記ページからどうぞ。
◆X線作業主任者の過去問の解説:管理(2021年4月)
◆X線作業主任者の過去問の解説:法令(2021年4月)
◆X線作業主任者の過去問の解説:測定(2021年4月)
◆X線作業主任者の過去問の解説:生体(2021年4月)
問1 エックス線に関する次の記述のうち、正しいものはどれか。
(1)エックス線は、エックス線管の陰極と陽極の間に高電圧をかけて発生させる高エネルギーの荷電粒子の流れである。
(2)エックス線は、磁場の影響を受ける。
(3)エックス線は、直接電離放射線である。
(4)連続エックス線は、高エネルギー電子が原子核近傍の強い電場を通過するとき急に減速され、運動エネルギーの一部を電磁波の形で放出するものである。
(5)エックス線のエネルギーは、その波長に比例する。
(1)は誤り。エックス線は、電磁波です。一方、アルファ線やベータ線は、荷電粒子の流れです。
(2)は誤り。電荷を持たないエックス線は、電場や磁場の影響を受けません。
(3)は誤り。エックス線は、電荷を持たない「間接電離放射線」です。
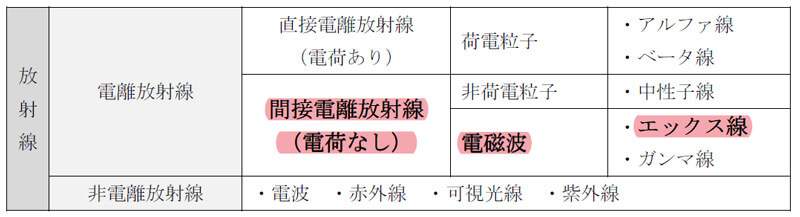
一般的に放射線は、原子の電離作用を持つ電離放射線のことを指しますが、可視光線などの非電離放射線を含めることもあります。
電荷を持つ電離放射線を直接電離放射線といい、電荷を持たない電離放射線を間接電離放射線といいます。
主な放射線の分類は下記表をご覧ください。
(4)は正しい。
(5)は誤り。エックス線のエネルギーと波長は、「反比例」の関係にあります。例えば、エックス線のエネルギーが大きくなれば、その波長は短くなります。
問2 エックス線装置の管電流を一定にして、管電圧を増加させた場合に、発生する連続エックス線に認められる変化として、誤っているものは次のうちどれか。
(1)最大エネルギーは、高くなる。
(2)最大強度を示す波長は、短くなる。
(3)線質は、硬くなる。
(4)全強度は、管電圧に比例して大きくなる。
(5)発生効率は、管電圧に比例して大きくなる。
(1)(2)(3)(5)は正しい。
(4)は誤り。全強度は管電圧の「2乗」に比例して増加します。
問3 特性エックス線に関する次の記述のうち、正しいものはどれか。
(1)特性エックス線の波長は、ターゲット元素の原子番号が大きくなると長くなる。
(2)ターゲット元素がタングステンの場合のK励起電圧は、タングステンより原子番号の小さい銅やモリブデンの場合に比べて高い。
(3)管電圧がK励起電圧を下回るときは、K系列以外の系列の特性エックス線も発生することはない。
(4)K殻電子が電離されたことによって特性エックス線が発生することをオージェ効果という。
(5)特性エックス線は、原子核のエネルギー準位の遷移に伴い、原子核から放出される。
(1)は誤り。特性エックス線の波長は、ターゲット元素の原子番号を大きくすると「短く」なります。
(2)は正しい。
(3)は誤り。管電圧が、K系列の特性エックス線を発生させるのに必要な最小値であるK励起電圧を下回るときでも、他の系列の特性エックス線が発生することがあります。
(4)は誤り。オージェ効果とは、電磁波として特性エックス線を放出する代わりに、そのエネルギーをより外側にある軌道電子に与えて、電子を原子の外に放出する現象をいいます。
(5)は誤り。特性エックス線は、軌道電子がエネルギー準位の高い軌道から低い軌道へと転移(遷移)するとき発生します。
問4 エックス線と物質との相互作用に関する次の記述のうち、誤っているものはどれか。
(1)入射エックス線のエネルギーが中性子1個の静止質量に相当するエネルギー以上にならないと、電子及び陽電子を生じる電子対生成が起こらない。
(2)コンプトン効果とは、エックス線光子と原子の軌道電子とが衝突し、電子が原子の外に飛び出し、光子が運動の方向を変える現象である。
(3)コンプトン効果による散乱エックス線は、入射エックス線のエネルギーが高くなるほど前方に散乱されやすくなる。
(4)光電効果とは、原子の軌道電子がエックス線光子のエネルギーを吸収して原子の外に飛び出し、光子が消滅する現象である。
(5)光電効果が起こる確率は、エックス線のエネルギーが高くなるほど低下する。
(1)は誤り。電子対生成は、入射エックス線のエネルギーが、「電子2個」の静止質量に相当する1.02MeV以上であるときに生じます。
(2)(3)(4)(5)は正しい。
問5 あるエックス線装置のエックス線管の焦点から1m離れた点での1cm線量当量率は60mSv/hであった。
このエックス線装置を用いて、鉄板とアルミニウム板を重ね合わせた板に細い線束のエックス線を照射したとき、エックス線管の焦点から1m離れた点における透過後の1cm線量当量率は7.5mSv/hであった。
このとき、鉄板とアルミニウム板の厚さの組合せとして正しいものは次のうちどれか。
ただし、このエックス線に対する鉄の減弱係数を3.0cm-1、アルミニウムの減弱係数を0.5cm-1とし、鉄板及びアルミニウム板を透過した後のエックス線の実効エネルギーは、透過前と変わらないものとし、散乱線による影響は無いものとする。
なお、loge2=0.69とする。
A:鉄板 B:アルミニウム板
(1)A:2.3mm B:13.8mm
(2)A:2.3mm B:20.7mm
(3)A:4.6mm B:13.8mm
(4)A:4.6mm B:20.7mm
(5)A:4.6mm B:27.6mm
答え(3)
この問題では、半価層と減弱係数の関係式と減弱の式を用いて、鉄板とアルミニウム板の厚さの組合せを求めます。
まず、それぞれの金属板の半価層を、半価層と減弱係数の関係式μh = loge2 ≒ 0.69を使って求めましょう。
ここでは、それぞれの半価層を区別するために、鉄板の半価層をhaとし、アルミニウム板の半価層をhbとします。
問題文のただし書きの前半部分にある「ただし、このエックス線に対する鉄の減弱係数を3.0cm-1、アルミニウムの減弱係数を0.5cm-1」よりそれぞれの金属板の減弱係数を用いて計算します。
先に、鉄板の半価層haを求めます。
問題文の最後「なお、loge2=0.69とする。」の部分より「μh = 0.69」として計算します。
3.0 [cm-1] × ha [cm] = 0.69
ha [cm] = 0.69 / 3.0 [cm-1]
ha [cm] = 0.23 [cm]
最終的に求めたい厚さの単位はmmなので、mm単位に直すと次のようになります。
ha [mm] = 0.23 [cm] × 10 = 2.3 [mm]
つまり、鉄板の半価層haは、2.3 mmだとわかります。
次に、アルミニウム板の半価層hbを求めます。
問題文の最後「なお、loge2=0.69とする。」の部分より「μh = 0.69」として計算します。
0.5 [cm-1] × hb [cm] = 0.69
hb [cm] = 0.69 / 0.5 [cm-1]
hb [cm] = 1.38 [cm]
最終的に求めたい厚さの単位はmmなので、mm単位に直すと次のようになります。
hb [mm] = 1.38 [cm] × 10 = 13.8 [mm]
つまり、アルミニウム板の半価層hbは、13.8 mmだとわかります。
それぞれの金属板の半価層がわかったので、減弱の式 I = I0 (1/2) x/hを使って「鉄板とアルミニウム板を重ね合わせた板に細い線束のエックス線を照射したとき、エックス線管の焦点から1m離れた点における透過後の1cm線量当量率が7.5mSv/h」になる、「鉄板とアルミニウム板の厚さの組合せ」を求めます。
ここでは、それぞれの板の厚さを区別するために、鉄板の厚さをxaとし、アルミニウム板の厚さをxbとします。
ここで、問題文と計算で得た数値を整理しておきます。
① 問題文より、金属板を透過前の1 cm線量当量率は60 mSv/h、透過後は7.5 mSv/hです。
② 鉄板の厚みはxa mm、半価層は2.3 mmです。
③ アルミニウム板の厚みはxb mm、半価層は13.8 mmです。
また、今回のように、複数の板を重ね合わせる場合、減弱割合の積(掛け算)となるので次の式になります。
I=I0 (1/2) xa / ha × (1/2) xb / hb
では、この式にそれぞれの数値を代入し、計算します。
7.5 [mSv/h] = 60 [mSv/h] × (1/2) xa [mm] / 2.3 [mm] × (1/2) xb [mm] / 13.8 [mm]
7.5 [mSv/h] / 60 [mSv/h] = (1/2) xa [mm] / 2.3 [mm] × (1/2) xb [mm] / 13.8 [mm]
(1/8) = (1/2) xa [mm] / 2.3 [mm] × (1/2) xb [mm] / 13.8 [mm]
(1/2) × (1/2) × (1/2) = (1/2) xa [mm] / 2.3 [mm] × (1/2) xb [mm] / 13.8 [mm]
(1/2)3 = (1/2) xa [mm] / 2.3 [mm] × (1/2) xb [mm] / 13.8 [mm]
(1/2)3 = (1/2) (xa [mm] / 2.3 [mm]) + (xb [mm] / 13.8 [mm])
左辺と右辺は、(1/2)の部分が同じなので、左辺の指数3と、右辺の指数は同じ数値になります。
指数の部分を抜き出すと、次のようになります。
3 = (xa [mm] / 2.3 [mm]) + (xb [mm] / 13.8 [mm])
続いて、問題の選択肢から適切な数値を選ぶと、xa=4.6 mm、xb=13.8 mmが適切であることがわかります。
確認のため、代入すると次のようになります。
(1/2)3 = (1/2)4.6 [mm] / 2.3 [mm] × (1/2)13.8 [mm] / 13.8 [mm]
(1/2)3 = (1/2)2 × (1/2)1
(1/2)3 = (1/2)2 + 1
(1/2)3 = (1/2)3
したがって、(3)A:4.6mm B:13.8mmが正解になります。
問6 あるエネルギーのエックス線に対する半価層が5mmの遮へい板P、10mmの遮へい板Q、15mmの遮へい板Rがあり、板厚はともに10mmである。
これらを用いた次のAからDの遮へい体により、このエックス線を遮へいするとき、遮へい効果の高いものから順に並べたものは(1)~(5)のうちどれか。
A 遮へい板Pを2枚重ねた遮へい体
B 遮へい板Qを3枚重ねた遮へい体
C 遮へい板P1枚と遮へい板R2枚を重ねた遮へい体
D 遮へい板P1枚と遮へい板Q1枚と遮へい板R1枚を重ねた遮へい体
(1)A > C > B > D
(2)A > D > C > B
(3)B > A > C > D
(4)B > C > D > A
(5)C > D > A > B
答え(2)
この問題では、減弱の式を用いて、A、B、C、Dそれぞれの遮へい体のパターンについて、遮へい効果の高いものから順に並べたものを選択します。
今回のように、複数の遮へい体を重ね合わせる場合、減弱割合の積(掛け算)となるので次の式を用います。
▼遮へい体を2枚重ねた場合
I=I0 (1/2) xa / ha × (1/2) xb / hb
▼遮へい体を3枚重ねた場合
I=I0 (1/2) xa / ha × (1/2) xb / hb × (1/2) xc / hc
まず、A(遮へい板Pを2枚重ねた遮へい体)の遮へい体の遮へい効果を求めます。
I=I0 (1/2) 10 [mm] / 5 [mm] × (1/2) 10 [mm] / 5 [mm]
I=I0 (1/2) 2 × (1/2) 2
I=I0 (1/2) 4
続いて、B(遮へい板Qを3枚重ねた遮へい体)の遮へい体の遮へい効果を求めます。
I=I0 (1/2) 10 [mm] / 10 [mm] × (1/2) 10 [mm] / 10 [mm] × (1/2) 10 [mm] / 10 [mm]
I=I0 (1/2) 1 × (1/2) 1 × (1/2) 1
I=I0 (1/2) 3
続いて、C(遮へい板P1枚と遮へい板R2枚を重ねた遮へい体)の遮へい体の遮へい効果を求めます。
I=I0 (1/2) 10 [mm] / 5 [mm] × (1/2) 10 [mm] / 15 [mm] × (1/2) 10 [mm] / 15 [mm]
I=I0 (1/2) 2 × (1/2) 0.66… × (1/2) 0.66…
I=I0 (1/2) 3.33…
最後に、D(遮へい板P1枚と遮へい板Q1枚と遮へい板R1枚を重ねた遮へい体)の遮へい体の遮へい効果を求めます。
I=I0 (1/2) 10 [mm] / 5 [mm] × (1/2) 10 [mm] / 10 [mm] × (1/2) 10 [mm] / 15 [mm]
I=I0 (1/2) 2 × (1/2) 1 × (1/2) 0.66…
I=I0 (1/2) 3.66…
(1/2)の右上の指数の値が大きいほど、遮へい効果が高くなります。
したがって、(2)A > D > C > Bが正解です。
問7 エックス線の散乱に関する次の文中の[ ]内に入れるAからCの語句又は数値の組合せとして、正しいものは(1)~(5)のうちどれか。
「エックス線装置を用い、管電圧200kVで、厚さが20mmの鋼板及びアルミニウム板のそれぞれにエックス線のビームを垂直に照射し、散乱角135°方向の後方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、[ A ]の後方散乱線の方が大きかった。
次に、同じ照射条件で、鋼板について、散乱角120°及び135°の方向の後方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、[ B ]の方向の方が大きかった。
また、同じ照射条件で、鋼板について、散乱角30°及び60°の方向の前方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、[ C ]の方向の方が大きかった。」
(1)A:アルミニウム板 B:120° C:60°
(2)A:アルミニウム板 B:135° C:30°
(3)A:アルミニウム板 B:135° C:60°
(4)A:鋼板 B:120° C:60°
(5)A:鋼板 B:135° C:30°
この問題では、諸条件を変えたときに、エックス線の散乱がどのようになるかを答えます。
確実に正解するために、ポイントを押さえましょう。
[A]後方散乱線の空気カーマ率は、照射する物体を「鋼板」と「アルミニウム板」で比較すると「アルミニウム板」の方が大きくなります。
[B]後方散乱線の空気カーマ率は、散乱角「120°」と「135°」で比較すると「135°」の方が大きくなります。
[C]前方散乱線の空気カーマ率は、散乱角「30°」と「60°」で比較すると「30°」の方が大きくなります。
問8 エックス線を利用した各種試験装置に関する次の記述のうち、誤っているものはどれか。
(1)蛍光エックス線分析装置は、物質を透過したエックス線を蛍光体を塗布した板の上に当てたときにできる蛍光像を観察することによって、物質の欠陥の程度などを識別する装置である。
(2)エックス線マイクロアナライザーは、細く絞った電子線束を試料の微小部分に照射し、発生する特性エックス線を分光することによって、微小部分の元素を分析する装置である。
(3)エックス線回折装置は、結晶質の物質にエックス線を照射すると特有の回折像が得られることを利用して、物質の結晶構造を解析し、物質の性質を調べる装置である。
(4)エックス線応力測定装置は、応力による結晶の面間隔の変化をエックス線の回折を利用して調べることにより、物質内の残留応力の大きさを測定する装置である。
(5)エックス線透過試験装置は、被検査物体を透過したエックス線による画像を観察する装置で、画像の検出にはフィルムなどが用いられる。
(1)は誤り。蛍光エックス線分析装置は、白色エックス線を試料に照射し、生ずる蛍光エックス線の性質を調べ、試料の定性、定量分析を行う装置です。
(2)(3)(4)(5)は正しい。
問9 単一エネルギーで太い線束のエックス線が物質を透過するときの減弱及び再生係数(ビルドアップ係数)に関する次の記述のうち、誤っているものはどれか。
(1)再生係数は、入射エックス線の線量率が高くなるほど小さくなる。
(2)再生係数は、物質への照射面積が大きいほど大きくなる。
(3)再生係数は、物質の厚さが薄くなるほど小さくなる。
(4)再生係数は、透過後、物質から離れるほど小さくなり、その値は1に近づく。
(5)太い線束のエックス線では、散乱線が加わるため、細い線束のエックス線より減弱曲線の勾配は緩やかになり、見かけ上、減弱係数が小さくなる。
(1)は誤り。再生係数は、入射エックス線の線量率の影響を受けません。
(2)(3)(4)(5)は正しい。
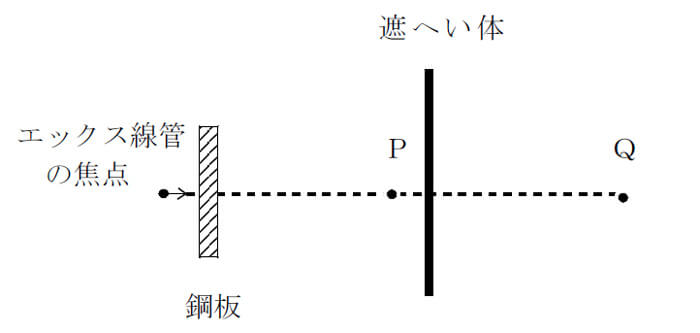
問10 下図のようにエックス線装置を用いて鋼板の透過写真撮影を行うとき、エックス線管の焦点から4mの距離にあるP点における写真撮影中の1cm線量当量率は、160μSv/hである。
この装置を使って、露出時間が1枚につき2分の写真を週300枚撮影するとき、P点の後方に遮へい体を設けることにより、エックス線管の焦点からP点の方向に8mの距離にあるQ点が管理区域の境界線上にあるようにすることのできる遮へい体の厚さは、次のうちどれか。
ただし、遮へい体の半価層は15mmとし、3か月は13週とする。
(1)10mm
(2)15mm
(3)20mm
(4)25mm
(5)30mm
答え(5)
この問題では、距離の逆2乗則と減弱の式を用いて、遮へい体の厚さを求めます。
まず、問題文で与えられている値から3か月の全照射時間を計算します。
なお、3か月単位にするのは、管理区域が1.3mSv/3か月を超えるおそれのある区域だからです。
照射時間=露出時間[min/枚]×週の撮影枚数[枚/週]×3か月の週数[週/3か月]
=2[min/枚]×300[枚/週]×13[週/3か月]
=7,800[min/3か月]
次の計算をしやすくするために、分単位から時間単位に直します。
7,800[min/3か月]÷60[min/h]=130[h/3か月]
この3か月の全照射時間にP点における写真撮影中の1cm線量当量率「160μSv/h」を掛けて3か月あたりの1cm線量当量率を求めます。
130[h/3か月]×160[μSv/h]=20,800[μSv/3か月]
次の計算をしやすくするために、μSv/3か月単位からmSv/3か月単位に直します。
20,800[μSv/3か月]÷1,000[μSv/mSv]=20.8[mSv/3か月]
続いて、距離の逆2乗則を用いて、焦点から8mの距離にあるQ点の3か月当りの1cm線量当量率を計算します。
なお、ここではQ点の3か月当りの1cm線量当量率をAとします。
A[mSv/3か月]/20.8[mSv/3か月]=42[m]/82[m]
A[mSv/3か月]=16[m]×20.8[mSv/3か月])/64[m]
A[mSv/3か月]=5.2[mSv/3か月]
続いて、今求めた「Q点の3か月当りの1cm線量当量率5.2mSv/3月」と「管理区域の境界の線量率1.3mSv/3月」、問題文ただし書きの「遮へい体の半価層は15mm」を、減弱の式に代入して、「エックス線管の焦点からP点の方向に8mの距離にあるQ点が管理区域の境界線上にあるようにすることのできる遮へい体の厚さ」を計算します。
なお、ここでは遮へい体の厚さをxとします。
1.3[mSv/3か月]=5.2[mSv/3か月] × (1/2)x[mm]/15[mm]
1.3[mSv/3か月]/5.2[mSv/3か月]=(1/2)x[mm]/15[mm]
1/4=(1/2)x[mm]/15[mm]
1/2×1/2=(1/2)x[mm]/15[mm]
(1/2)2=(1/2)x[mm]/15[mm]
左辺と右辺の指数の部分を抜き出すと次のようになります。
2=x[mm]/15[mm]
x[mm]=30[mm]
したがって、遮へい体の厚さは(5)30mmが正解です。
-
同カテゴリーの最新記事
- 2024/10/10:X線作業主任者の過去問の解説:管理(2024年10月)
- 2024/04/10:X線作業主任者の過去問の解説:管理(2024年4月)
- 2022/04/10:X線作業主任者の過去問の解説:管理(2022年4月)
- 2021/10/10:X線作業主任者の過去問の解説:管理(2021年10月)
- 2021/04/10:X線作業主任者の過去問の解説:管理(2021年4月)










